2019-ben a Nobel-díjas Terence Tao majdnem megoldotta a 3x+1 matematikai problémát. De a végén ő is elbukott.
A 3x+1 matematikai problémát, vagyis a Collatz-sejtést 1937-ben fogalmazta meg Lothar Collatz német matematikus. Ez egy máig megoldatlan probléma a matematikában.
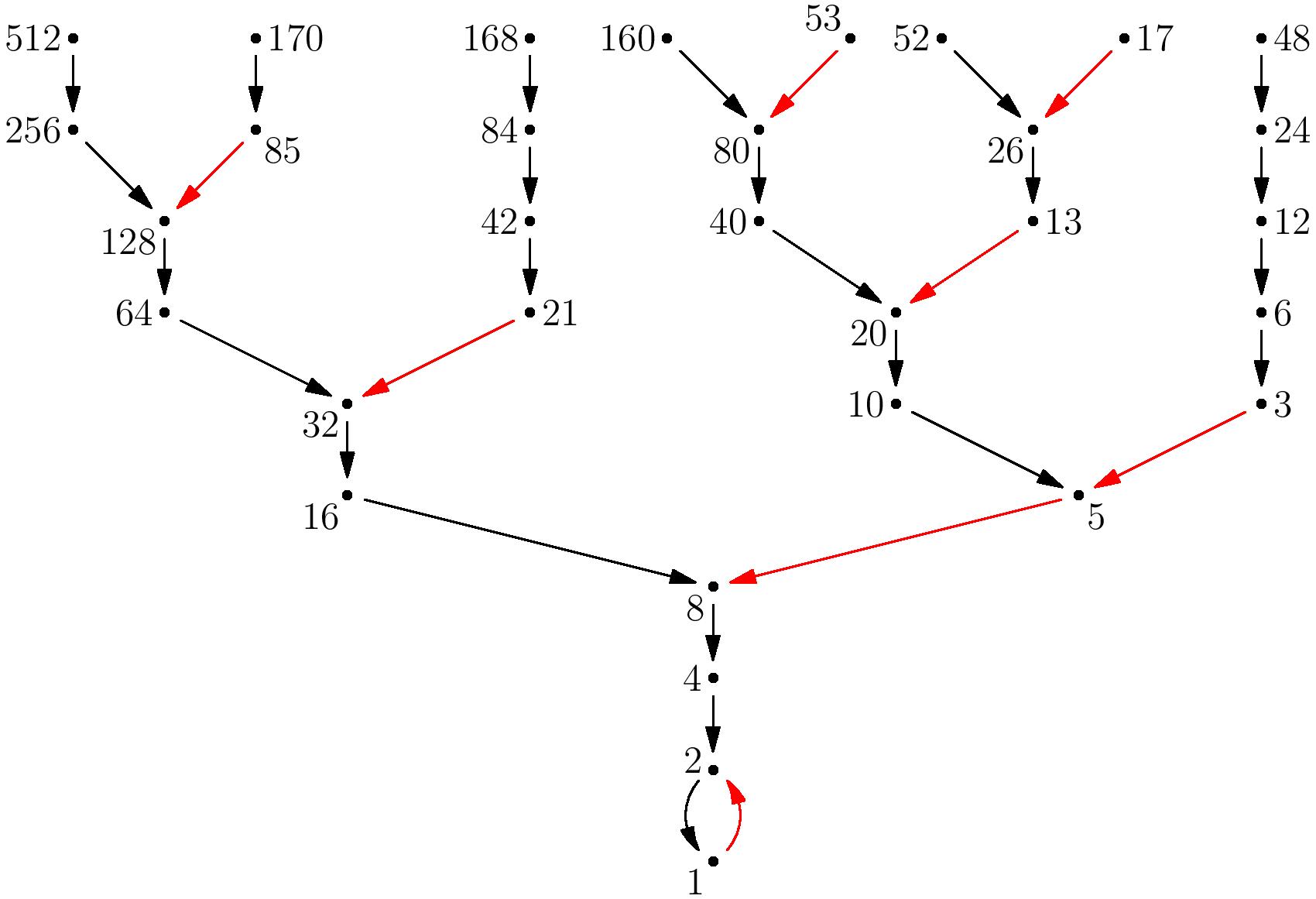
Nehezen tudnánk saját szavainkkal megfogalmazni, miről is szól pontosan, ezért inkább a Wikipediát idézzük:
A probléma a következő: Tetszőleges pozitív egész számból kiindulva képezzünk végtelen sorozatot úgy, hogy ha a sorozat utoljára kiszámított eleme páros, akkor a rákövetkező elem ennek fele lesz, különben viszont a háromszorosánál eggyel nagyobb szám. Például ha a 7-ből indulunk ki (amely páratlan), akkor a rákövetkező elem 3×7+1=22, amely páros, így a következő elem a 22 fele, azaz 11 lesz. Tovább folytatva a szabály alkalmazását a 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1, … sorozatot kapjuk. Látható, hogy innentől a végtelenségig ismétlődik a 4, 2, 1 számhármas. Különböző számokból kiindulva azt tapasztaljuk, hogy újra meg újra olyan sorozatokat kapunk, amelyek a 4, 2, 1 számhármas végtelen ismétlődésébe torkollnak. A Collatz-sejtés azt mondja ki, hogy ez mindig így van: akármilyen pozitív számmal is kezdjük a sorozat képzését, a végén mindig a 4, 2, 1 ciklusba futunk bele.
A Collatz-sejtésről a hidegháború alatt az a pletyka/vicc terjedt, hogy az valójában egy szovjet „fegyver” az amerikai matematikai fejlődés lassítására, korábban ugyanis a Yale professzorai egy álló hónapon keresztül próbálták bizonyítani, sikertelenül.
A fiatal matematikusoknak ma már csak azt tanácsolják, hogy ne is vesztegessék az idejüket a Collatz-sejtésre, még úgy se, hogy ha valaki bebizonyítaná, az egymilliárd dollárt érne. Nézzük, hogy miért:










